“The most beautiful thing we can experience is the mysterious. It is the source of all true art and science.”
– Albert Einstein
Kaos. Ett ord som ofta kopplas till oreda, slump eller kaotiska livssituationer. Men inom matematiken betyder kaos något mycket mer specifikt: ett känsligt beroende av initialvillkor i deterministiska system. Detta blogginlägg är en djupdykning i kaosteori, där vi inte bara förklarar vad det handlar om – vi simulerar det med kod i en Jupyter Notebook.
Vi hämtar vår inspiration från en av de mest inflytelserika böckerna i ämnet:
📘 Nonlinear Dynamics and Chaos av Steven Strogatz.
🧠 Vad är kaosteori?
Kaosteori är en gren av matematiken som behandlar icke-linjära dynamiska system – system där en liten förändring i initialvillkoren kan leda till dramatiskt olika resultat.
Exempel:
- Atmosfären (väderförändringar)
- Populationer i ekologi
- Elektriska kretsar
- Pendlar och gungor
Alla dessa är exempel på system som kan uppvisa kaotiskt beteende.
🔍 Från linjärt till icke-linjärt: En snabb översikt
Linjär matematik är enkel: resultatet är proportionellt mot insatsen.
Men verkligheten är inte alltid så enkel. De flesta naturliga fenomen är icke-linjära, vilket betyder att output inte är direkt proportionell till input.
När man analyserar dessa icke-linjära system upptäcker man ibland något överraskande:
- Regelbundenhet och mönster kan uppstå ur kaos.
- Små variationer i startpunkten kan ge dramatiskt olika banor.
- Det finns ofta ett underliggande deterministiskt system – trots att beteendet ser slumpmässigt ut.
📊 Exempel 1: Den logistiska ekvationen – kaosets inkörsport
En av de enklaste modellerna som uppvisar kaotiskt beteende är den logistiska ekvationen:
CopyEditxₙ₊₁ = r * xₙ * (1 - xₙ)
Detta är en rekursiv funktion som används inom befolkningsdynamik.
xₙär andelen av den maximala populationen vid tidpunktnrär tillväxtparametern
🔧 Kodexempel i Jupyter Notebook
📦 Först: installera nödvändiga bibliotek (om du inte har dem):
bashCopyEditpip install matplotlib numpy
🔢 Simulera logistisk karta:
pythonCopyEditimport numpy as np
import matplotlib.pyplot as plt
def logistic_map(r, x, n):
results = []
for i in range(n):
x = r * x * (1 - x)
results.append(x)
return results
r_values = [2.5, 3.2, 3.5, 3.9]
x0 = 0.5
n = 100
plt.figure(figsize=(12, 8))
for r in r_values:
x = logistic_map(r, x0, n)
plt.plot(range(n), x, label=f"r = {r}")
plt.title("Logistisk karta för olika r-värden")
plt.xlabel("Iteration")
plt.ylabel("x")
plt.legend()
plt.grid(True)
plt.show()
🧭 Exempel 2: Lorenzsystemet – fjärilseffekten i praktiken
Lorenzsystemet är tre kopplade, icke-linjära differentialekvationer:
latexCopyEdit\begin{aligned}
\frac{dx}{dt} &= \sigma(y - x) \\
\frac{dy}{dt} &= x(\rho - z) - y \\
\frac{dz}{dt} &= xy - \beta z
\end{aligned}
Där σ, ρ, β är konstanter.
📦 Kod för att simulera Lorenzsystemet
🧰 Installera:
bashCopyEditpip install scipy matplotlib
🌀 Kör simuleringen:
pythonCopyEditfrom scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def lorenz(t, state, sigma=10, rho=28, beta=8/3):
x, y, z = state
dxdt = sigma * (y - x)
dydt = x * (rho - z) - y
dzdt = x * y - beta * z
return [dxdt, dydt, dzdt]
initial_state = [1.0, 1.0, 1.0]
t_span = (0, 50)
t_eval = np.linspace(*t_span, 10000)
solution = solve_ivp(lorenz, t_span, initial_state, t_eval=t_eval)
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
ax.plot(solution.y[0], solution.y[1], solution.y[2], lw=0.5)
ax.set_title("Lorenz-attractor – Kaotiskt men deterministiskt")
plt.show()
🎯 Känslighet för initialvillkor
Testa att ändra initial_state från [1.0, 1.0, 1.0] till [1.01, 1.0, 1.0].
Trots den lilla ändringen avviker banan snabbt – detta är fjärilseffekten i praktiken.
📈 Exempel 3: Bifurkationsdiagram för logistiska kartan
Diagrammet visar hur långsiktigt beteende förändras beroende på r-värde:
pythonCopyEditr_values = np.linspace(2.5, 4.0, 10000)
n = 1000
last = 100
x = 1e-5 * np.ones_like(r_values)
r_plot = []
x_plot = []
for i in range(n):
x = r_values * x * (1 - x)
if i >= (n - last):
r_plot.extend(r_values)
x_plot.extend(x)
plt.figure(figsize=(14, 8))
plt.plot(r_plot, x_plot, ',k', alpha=0.25)
plt.title("Bifurkationsdiagram för logistiska kartan")
plt.xlabel("r")
plt.ylabel("x")
plt.show()
🧠 Vad vi lär oss
- Kaos = deterministiskt men känsligt
- Små förändringar får stor effekt
- Visualisering gör kaosteori mer intuitivt
- Bifurkationer visar strukturen i det kaotiska
🔬 Mer att utforska
📌 Andra kaotiska system du kan simulera:
- Driven pendel (icke-linjär)
- Rössler attractor
- Duffing oscillator
- Henon map
📚 Rekommenderade böcker:
- Nonlinear Dynamics and Chaos – Steven Strogatz
- Chaos: Making a New Science – James Gleick
- The Essence of Chaos – Edward Lorenz
🎓 Nästa steg
- Kör dessa kodexempel i Jupyter Notebook
- Ändra parametrar – se hur känsligt systemet reagerar
- Lägg till sliders (interaktivt med
ipywidgets) - Exportera till animation eller video
✅ Sammanfattning
Att simulera kaosteori med Python i Jupyter Notebook är ett kraftfullt sätt att förstå icke-linjära system. Genom att leka med initialvärden, parametrar och visualiseringar, får du en intuitiv känsla för hur kaos fungerar. Och det bästa? Du behöver inte vara expert – bara nyfiken!
Gillade du detta blogginlägg? Kommentera nedan eller kontakta mig för en färdig .ipynb-fil!
📌 Taggar: #kaosteori #python #jupyternotebook #lorenzsystem #logistiskekvation #strogatz #dynamiskasystem
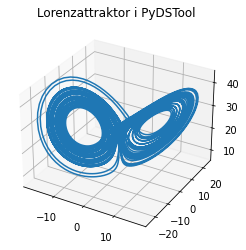
Bonus:
mer kod:
from PyDSTool import *
import matplotlib.pyplot as plt
Parametrar för Lorenzsystemet
pars = {’sigma’:10.0, ’beta’:8/3, ’rho’:28.0}
icdict = {’x’:2.0, ’y’:1.0, ’z’:30.0}
vardict = {’x’:’sigma(y – x)’, ’y’:’x(rho – z) – y’, ’z’:’xy – betaz’}
Skapa systemet
DSargs = args(name=’Lorenz’)
DSargs.pars = pars
DSargs.varspecs = vardict
DSargs.ics = icdict
DSargs.tdomain = [0, 50]
ode = Generator.Vode_ODEsystem(DSargs)
Kör simulering
traj = ode.compute(’lorenz’)
pts = traj.sample(dt=0.01)
Plotta
fig = plt.figure()
ax = fig.add_subplot(111, projection=’3d’)
ax.plot(pts[’x’], pts[’y’], pts[’z’])
ax.set_title(”Lorenzattraktor i PyDSTool”)
plt.show()
0 kommentarer